

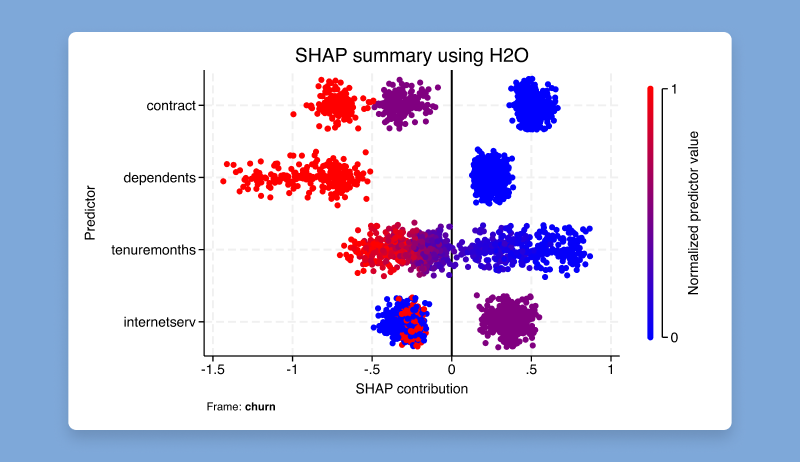
Machine learning methods are often used to solve research and business problems focused on prediction when the problems require more advanced modeling than linear or generalized linear models. Ensemble decision tree methods, which combine multiple trees for better predictions, are popular for such tasks. H2O is a scalable machine learning platform that supports data analysis and machine learning, including ensemble decision tree methods such as random forest and gradient boosting machine (GBM).
The new h2oml suite of Stata commands is a wrapper for H2O that provides end-to-end support for H2O machine learning analysis using ensemble decision tree methods. After using the h2o commands to initiate or connect to an existing H2O cluster, you can use the h2oml commands to perform GBM and random forest for regression and classification problems. The h2oml suite offers tools for hyperparameter tuning, validation, cross-validation, evaluating model performance, obtaining predictions, and explaining these predictions. For example,
Initiate H2O from within Stata
. h20 init
Import data from Stata into H2O
. _h20frame put, into(dataframe) current
Perform gradient boosting binary classification, and tune the number of trees and hyperparameters
. h2oml gbbinclass response predictors, ntrees(20(10)200) lrate(0.1(0.1)1)
Assess variable importance
. h2omlgraph varimp
Make predictions
. _h2oframe change newdata
. h20mlpredict outcome_pred
And there’s much more.
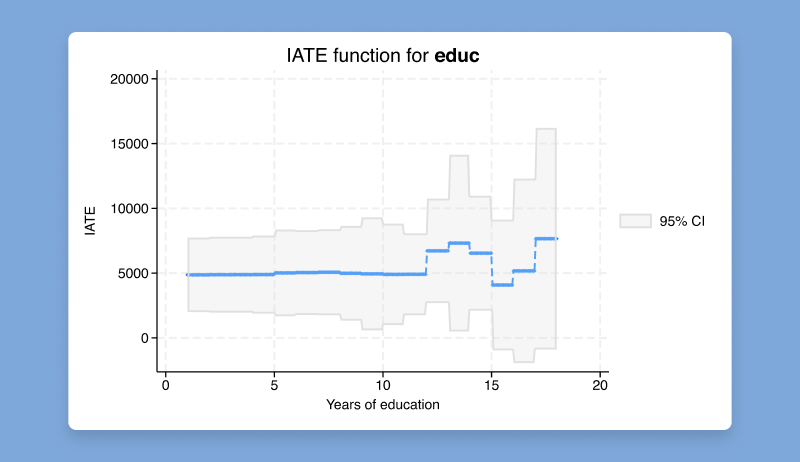
Treatment effects estimate the causal effect of a treatment on an outcome. This effect may be constant or it may vary across different subpopulations. Researchers are often interested in whether and how treatment effects differ.
A labor economist may want to know the effect of a job training program on earnings only for those who participate in the program.
An online shopping company may want to know the effect of a price discount on purchasing behavior for customers with different demographic characteristics, such as age and income.
A medical team may want to measure the effect of smoking on stress levels for individuals in different age groups.
With the new cate command, you can go beyond estimating an overall treatment effect to estimating individualized or group-specific ones that address these types of research questions.
The cate command can estimate three types of CATEs: individualized average treatment effects, group average treatment effects, and sorted group average treatment effects. Beyond estimation, the cate suite provides features to predict, visualize, and make inferences about the CATEs.

You can now absorb not just one, but multiple high-dimensional categorical variables in your linear regression, with or without fixed effects, and in linear models accounting for endogeneity using two-stage least squares. This is useful when you want your model to be adjusted for these variables but estimating their effect is not of interest and is computationally expensive.
The areg, xtreg, fe, and ivregress 2sls commands now allow the absorb() option to be specified with multiple categorical variables. Previously, areg allowed only one variable in absorb(), while xtreg, fe and ivregress 2sls did not allow the option.
For example, we could fit a regression model that adjusts for three high-dimensional categorical c1, c2, and c3 predictors by typing
. areg y x, absorb(c1 c2 c3)
If we wanted to absorb these variables in a fixed-effects model, we can do that, too:
. xtset panelvar
. xtreg y x, fe absorb(c1 c2 c3)
And in an instrumental-variables regression model, we can type
. ivregress 2sls y1 x1 (y2 x2), absorb(c1 c2 c3)
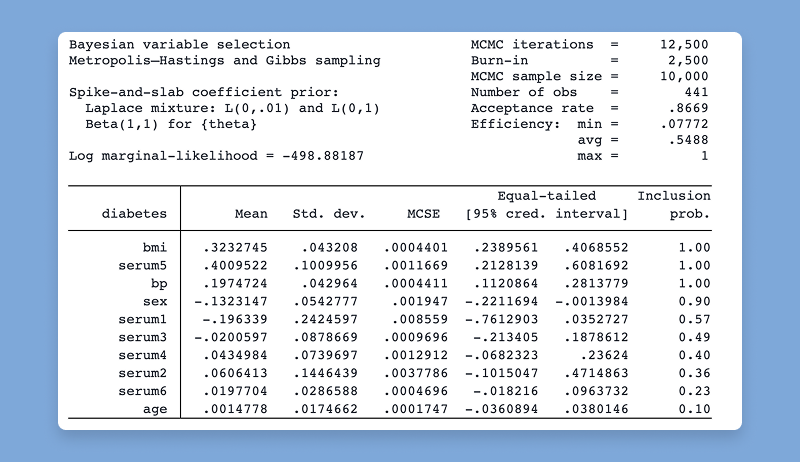
The new bayesselect command provides a flexible Bayesian approach to identify the subset of predictors that are most relevant to your outcome. It accounts for model uncertainty when estimating model parameters and performs Bayesian inference for regression coefficients. It uses a familiar syntax,
. bayesselect y x1-x100
As with other Bayesian regression procedures in Stata, posterior means, posterior standard deviations, Monte Carlo standard errors, and credible intervals of each predictor are reported for easy interpretation. Additionally, either inclusion coefficients or inclusion probabilities, depending on the selected prior, are included to indicate the importance of each predictor to model the outcome.
bayesselect is fully integrated in Stata's Bayesian suite and works seamlessly with all Bayesian postestimation routines, including prediction,
. bayesselect pmean, mean

Interval-censored multiple-event data commonly arise in longitudinal studies because each study subject may experience several types of events and those events are not observed directly but are known to occur within some time interval. For example, an epidemiologist studying chronic diseases might collect data on patients with multiple conditions, such as heart disease and metabolic disease, during different doctor visits. Similarly, a sociologist might conduct surveys to record major life events, such as job changes and marriages, at regular intervals.
You can now fit a marginal proportional hazards model for such data. The new stmgintcox command can accommodate single- and multiple-record-per-event data and supports time varying covariates for all events or specific ones.
For example, let’s say we have data on multiple events coded in the event variable that take place between times recorded in ltime and rtime and covariates x1-x3. We could simultaneously model the influence of covariates on time until each event using command
. stmgintcox x1 x2 x3, id(id) event(event) interval(ltime rtime)
From here, we could test the average effect of x1 across events by typing
. estat common x1
We could also graph survivor and other functions for both events,
. stcurve, survival
evaluate goodness of fit for each event,
. estat gofplot
and much more.
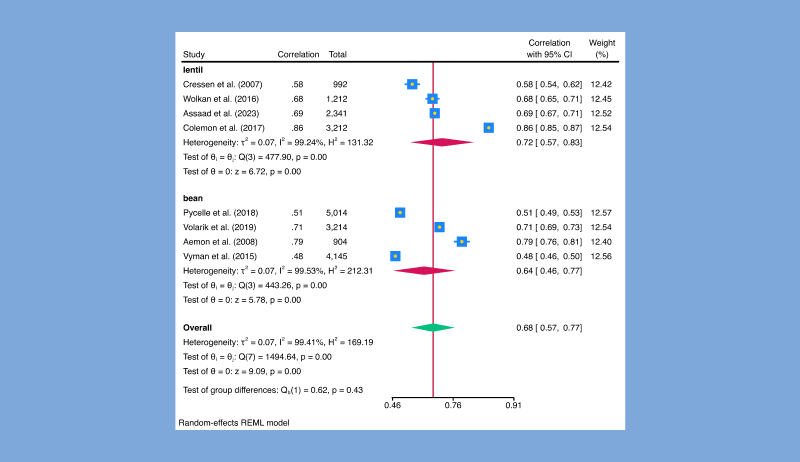
The meta suite now supports meta-analysis of correlation coefficients, allowing investigation of the strength and direction of relationships between variables across multiple studies. For instance, you may have studies reporting the correlation between education and income levels or between physical activity and improvements in mental health and wish to perform meta analysis.
Say variables corr and ntotal represent the correlation and the total number of subjects in each study, respectively. We can use these variables to declare our data using the meta esize command.
. meta esize corr ntotal, correlation studylabel(studylbl)
Because the variance of the untransformed correlation depends on the correlation itself, we may prefer to use the Fisher’s z-transformed correlation, a variance-stabilizing transformation particularly preferable when correlations are close to -1 or 1.
. meta esize corr ntotal, fisherz studylabel(studylbl)
All standard meta-analysis features, such as forest plots and subgroup analysis, are supported.
. meta forestplot, correlation

Easily fit CRE models to panel data with the new cre option of the xtreg command.
Consider the following commands to fit a CRE model with time-varying regressor x and time invariant regressor z:
. xtset panelvar
. xtreg y x z, cre vce(cluster panelvar)
A random-effects model may yield inconsistent estimates if there is correlation between the covariates and the unobserved panel-level effects. A fixed-effects model wouldn’t allow estimation of the coefficient on time-invariant regressor z. CRE models offer the best of both worlds.
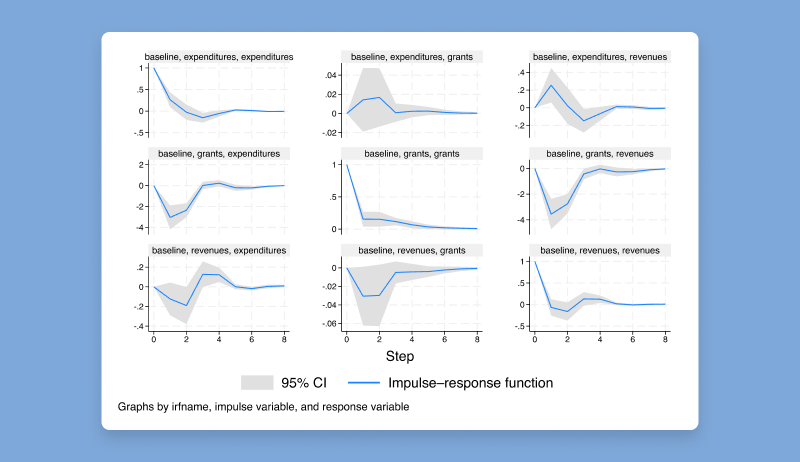
Fit vector autoregressive (VAR) models to panel data! Compute impulse–response functions, perform Granger causality tests and stability tests, include additional covariates, and much more. The new xtvar command has similar syntax and postestimation procedures as var, but it is appropriate for panel data rather than time-series data.
For example, we could fit a VAR model to a panel dataset with three outcomes of interest by typing
. xtset panelvar
. xtvar y1 y2 y3, lags(2)
Then, we can perform a Granger causality test,
. vargranger
or graph impulse–response functions.
. irf create baseline, set(irfs)
. irf graph irf
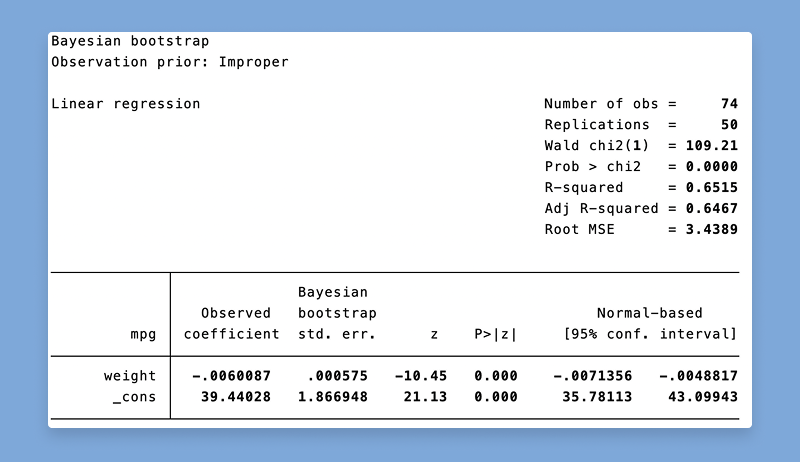
You can use the new bayesboot prefix to perform Bayesian bootstrap of statistics produced by official and community-contributed commands.
To compute a Bayesian bootstrap estimate of the mean of x, which is returned by summarize as r(mean), we type
. bayesboot r(mean): summarize x
You can also use the new rwgen command and new options for the bootstrap prefix to implement specialized bootstrap schemes. rwgen generates standard replication and Bayesian bootstrap weights. bootstrap has new fweights() and iweights() options for performing bootstrap replications using the custom weights. fweights() allows users to specify frequency weight variables for resampling, and iweights() lets users provide importance weight variables. These options extend bootstrap's flexibility by allowing user-supplied weights instead of internal resampling, making it easier to implement specialized bootstrap schemes and enhance reproducibility. bayesboot is a wrapper for rwgen and bootstrap that generates importance weights using Dirichlet distribution and applies these weights when bootstrapping.
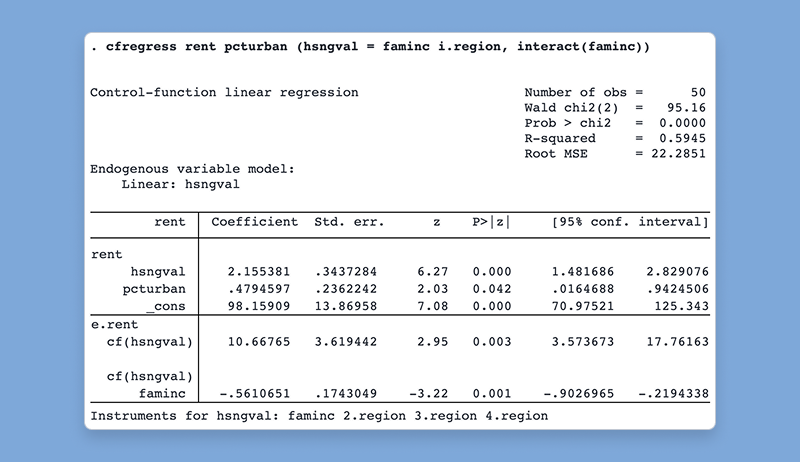
Fit control-function linear and probit models with the new cfregress and cfprobit commands. Control-function models offer a more flexible approach to traditional instrumental-variables (IV) methods by including the endogenous variable itself and its first-stage residual in the main regression; the residual term is called a control function.
For example, we could reproduce the estimates of a 2SLS IV regression,
. cfregress y1 x (y2 = z1 z2)
but we could also use a binary endogenous variable and include the interaction of the control function with z1,
. cfregress y1 x (y2bin = z1 z2, probit interact(z1))
Afterward, we could test for endogeneity by jointly testing the control function and the interaction.
. estat endogenous
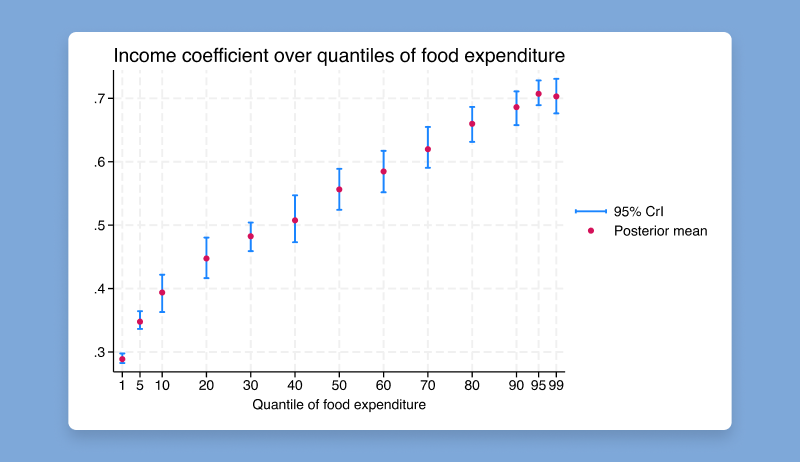
The qreg command for quantile regression is now compatible with the bayes prefix. In the Bayesian framework, we combine the asymmetric Laplace likelihood function with priors to provide full posterior distributions for quantile regression coefficients.
. bayes: qreg y x1 x2
Consequently, the asymmetric Laplace distribution is also a new likelihood function available in bayesmh.
. bayesmh y x1 x2, likelihood(asymlaplaceq({scale},0.5)) prior({y:}, normal(0,10000)) block({y:}) prior({scale}, igamma(0.01,0.01)) block({scale})
You can also use the asymmetric Laplace likelihood in bayesmh for random-effects quantile regression, simultaneous quantile regression, or to model nonnormal outcomes with pronounced skewness and kurtosis.
All implementations support standard Bayesian features, such as MCMC diagnostics, hypothesis testing, prediction.
. bayesgraph diagnostics

To estimate a linear regression of y1 on x1 and endogenous regressor y2 that is instrumented by z1 via 2SLS, we would type
. ivregress 2sls y1 x1 (y2 = z1)
When the instrument, z1, is only weakly correlated with the endogenous regressor, y2, inference can become unreliable even in relatively large samples. The new estat weakrobust postestimation command after ivregress performs Anderson–Rubin or conditional likelihood ratio (CLR) tests on the endogenous regressors. These tests are robust to the instrument being weak.
. estat weakrobust
This postestimation command supports all ivregresss estimators: 2sls, liml, and gmm.
The new ivsvar command estimates the parameters of SVAR models by using instrumental variables.
. ivsvar gmm y1 y2 (shock = z1 z2)
These estimated parameters can be used to trace out dynamic causal effects known as structural impulse–response functions (IRFs) using the familiar irf suite of commands.
. irf set ivsvar.irf
. irf create model1
. irf graph sirf, impulse(shock)
For multiple instruments, use the minimum distance estimator with ivsvar mdist, and specify how the instruments are related to the target shocks.
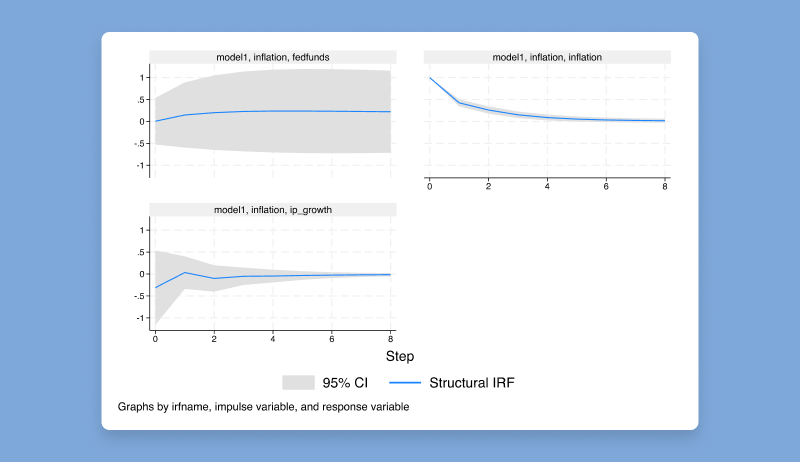
With the new ivlpirf command, you can account for endogeneity when using local projections to estimate dynamic causal effects.
Local projections are used to estimate the effect of shocks on outcome variables. When the shock of interest is on an impulse variable that may be endogenous, ivlpirf can be used to estimate the IRFs, and the impulse variable may be instrumented using one or more exogenous instruments.
For example, let’s say we are interested in estimating structural IRFs for the effects of an increase in x on y, using iv as an instrument for the endogenous impulse x:
. ivlpirf y, endogenous(x = iv)
We can then use the irf suite of commands to graph these IRFs:
. irf set ivlp.irf, replace
. irf create ivlp
. irf graph csirf

Use the new estat mundlak postestimation command after xtreg to choose between random-effects (RE) and fixed-effects (FE) or correlated random-effects (CRE) models. Unlike a Hausman test, we do not need to fit both the RE and FE models to perform a Mundlak test — we just need one! Again, consider the following model with time-varying regressor x and time invariant regressor z:
. xtreg y x z, vce(cluster clustvar)
. estat mundlak
The estat mundlak command tests the null hypothesis that x is uncorrelated with unobserved panel-level effects. Rejecting the hypothesis suggests that fitting an FE or CRE model that accounts for time-invariant unobserved heterogeneity is more sensible than an RE model.
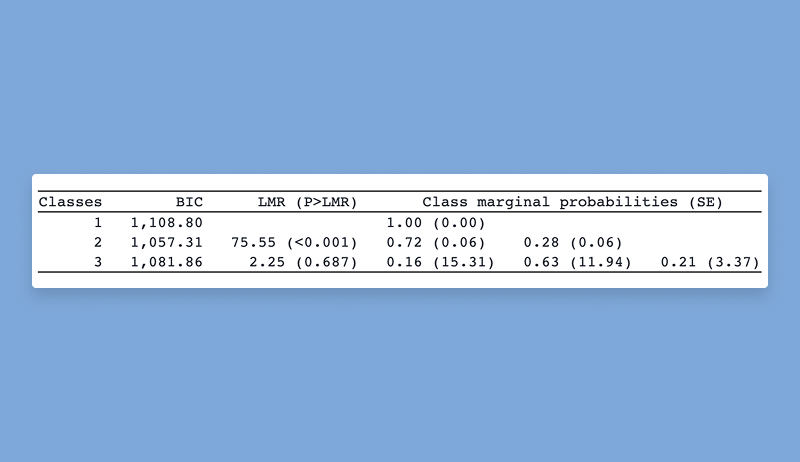
When you perform latent class analysis or finite mixture modeling, it is fundamental to determine the number of latent classes that best fits your data. With the new lcstats command, you can use statistics such as entropy and a variety of information criteria, as well as the Lo–Mendell–Rubin (LMR) adjusted likelihood-ratio test and Vuong–Lo–Mendell–Rubin (VLMR) likelihood-ratio test, to help you determine the appropriate number of classes. For example, you might fit one-class, two-class, and three-class models and store their results by typing
. gsem (y1 y2 y3 y4 <- ), logit lclass(C 1)
. estimates store oneclass
. gsem (y1 y2 y3 y4 <- ), logit lclass(C 2)
. estimates store twoclass
. gsem (y1 y2 y3 y4 <- ), logit lclass(C 3)
. estimates store threeclass
Then you can obtain model-comparison statistics and tests by typing
. lcstats
The lcstats command offers options for specifying which statistics and test to report and to customize the look of the table.
The Do-file Editor has the following additions:
Autocompletion of variable names, macros, and stored results. If you pause briefly as you type, suggestions of variable names from data in memory, macros, and stored results will appear in addition to the command names and existing words that appeared previously.
Do-file Editor templates. You can now save time and ensure consistency when you create new documents in the Do-file Editor by using Stata templates and user-defined templates.
Do-file Editor current word and selection highlighting. The Do-file Editor will now highlight all case-insensitive occurrences of the current word under the cursor and all case-sensitive occurrences of the current selection.
Bracket highlighting. The Do-file Editor will now highlight the brackets enclosing the current cursor position as you move through the document.
Code folding enhancements. You can now quickly fold all foldable blocks of code in your do-file by using the Fold all menu item. You can then selectively unfold your code one fold point at a time to show the more important parts of your do-file, or you can use the Do-file Editor’s Unfold all menu item to unfold every fold point. You can also select lines of code and transform them into a foldable block of code by using the Fold selection menu item. This can tidy up your code and increase the code’s readability. In addition, the code-folding feature has been changed to be less visually distracting by using arrow markers in the code-folding ribbon to indicate whether a code fold is expanded or collapsed and to hide expanded code-fold markers unless the user hovers the mouse over the code-folding ribbon.
Do-file Editor temporary and permanent bookmarks. The Do-file Editor now supports temporary bookmarks in addition to permanent bookmarks. The existing permanent bookmarks are saved as part of the do-file. You can use the new temporary bookmarks to immediately navigate your do-file but without making any changes to its content.
Show whitespace and tabs. The Do-file Editor can now show whitespace characters only within a selection instead of always showing them or not showing them at all.
Navigator panel. The Navigation control from previous releases of Stata has been replaced by the Navigator panel. It displays a list of permanent bookmarks and programs that are in a do-file. You can quickly jump to the position of a program or bookmark by double-clicking on the item in the Navigator panel. You can also delete and indent bookmarks from the Navigator panel.
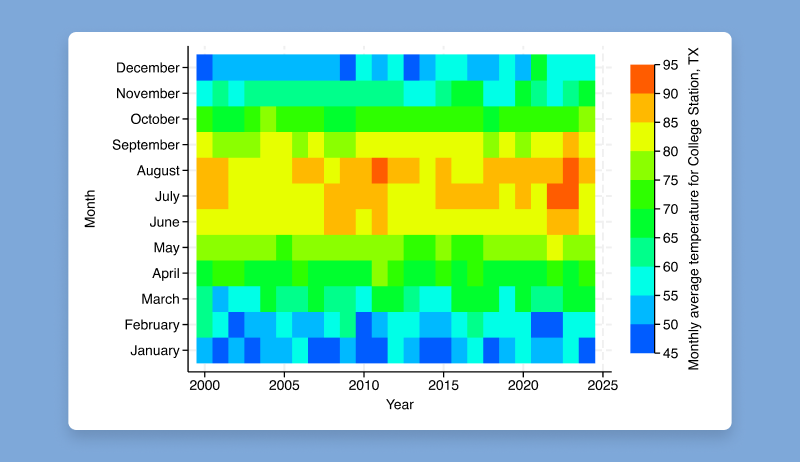
Stata 19 includes many new graphics features.
Heat maps. The new twoway heatmap command creates a heat map, which displays values of a numeric variable, z, across values of y and x as a grid of colored rectangles.
Range and point plot with capped spikes. The new twoway rpcap command plots points and range indicated by spikes with caps. These plots are useful for displaying a value of interest, such as a mean, and the corresponding confidence interval.
Range and point plot with spikes. The new twoway rpspike command plots points and ranges indicated by spikes. These plots are useful for displaying a value of interest, such as a mean, and the corresponding confidence interval.
Bar graphs with CIs, improved labeling, and control of bar groupings. graph bar now allows you to graph the mean and corresponding confidence interval. You can also use the new groupyvars option to group bars for the same y variable together. graph bar also has new options to control the ticks and labels on the categorical axis and to add a prefix or suffix to the bar labels.
Dot charts with CIs, improved labeling, and control of dot groupings. graph dot now allows you to graph the mean and corresponding confidence interval. You can also use the new groupyvars option to group dots for the same y variable together. graph dot also has new options to control the ticks and labels on the categorical axis.
Box plots with improved labeling and control of box groupings. You can also use the new groupyvars option to group boxes for the same y variable together. graph box also has new options to control the ticks and labels on the categorical axis.
Colors by variable for more graphs. The colorvar() option is now available with more twoway plots: line, connected, tsline, rline, rconnected, and tsrline. This option allows plots to vary color of lines, markers, and more based on the values of a specified variable.

Stata 19 also includes many additions that allow users to more easily create and customize tables.
Titles, notes, and exporting for tables. The table command is a flexible tool for creating tabulations, tables of summary statistics, tables of regression results, and more. It now allows you to add a title with the new title() option, to add a note with the new note() option, to control the appearance of the title and notes with the new titlestyles() and notestyles() options, and to export your table to your preferred document type (Word, LaTeX, Excel, etc.) with the new export() option.
Easier ANOVA tables. You can now more easily create and customize ANOVA tables after anova and oneway by collecting the new stored matrix r(ANOVA). You can use the new anova collection style to easily format these results in a standard ANOVA-style layout.
Better labels with collect get. With command collect get's new option commands(), you can specify the command names that posted the results being consumed. This allows collect get to search for command-specific result labels. The results in the collection will often have better labels, as they would if the collect prefix were used instead of the collect get command.
Determine layout of a collection. The new collect query layout command allows you to query a collection's layout specification. Previously, users typed collect layout to display both the layout and the table. Now you no longer need to see the full table each time you want to see the layout.
Control factor variables in headers. With collect style header's new option fvlevels(), you have more control over how factor variables appear in a table. Specify whether to hide or show factor-variable levels in row and column headers.
Remove results from a collection. The new collect unget command allows you to remove selected results from a collection. This can make it easier to lay out tables that do not involve these results.
Table-specific notes. The collect notes command has the new fortags() option that allows you to control which table should show the specified note.
Tabulations with measures of association and tests. You can now easily create customized tables with the results of tabulate and svy: tabulate. With the new collect() option, tabulated statistics are stored in a collection with its own layout and styles, which can be further customized and exported to a variety of file types. This is particularly useful when you wish to include cumulative percentages or measures of association from tabulate and tests from svy: tabulate.
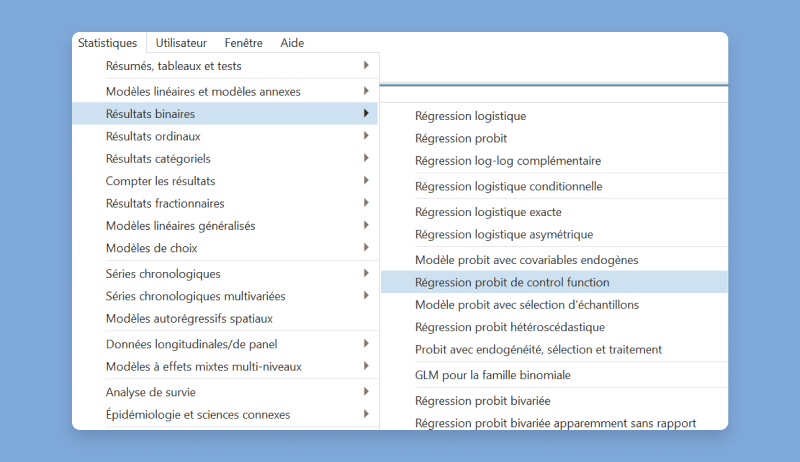
Stata's menus, dialogs, and the like can now be displayed in French.
If your computer language is set to French (fr), Stata will automatically use its French setting. To change languages manually using Windows or Unix, select Edit > Preferences > User interface language.... If you are using MacOS, select Stata 19 > Preferences > User-interface language.... You can also change the language from the command line by using the set locale_ui command.

The following features have also been added in Stata 19.